Question

A stack of cards consists of seven red and four blue cards. A second stack of cards consists of eleven red cards. A stack is selected at random and three of its cards are drawn. If all of them are red, what is the probability the rst stack was selected

Answer 1

0.1733 = 17.33% probability the first stack was selected.

Explanation:

To solve this question, it is needed to understand conditional probability, and the hypergeometric distribution.

Hypergeometric distribution:

The probability of x sucesses is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

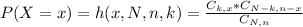
In which:

x is the number of sucesses.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Conditional probability:

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

Probability of all red cards for the first stack:

For this, we use the hypergeometric distribution, as the cards all chosen without replacement.

7 + 4 = 11 cards, which means that
`N = 11`.

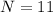7 red, which means that
`k = 7`

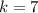
3 are chosen, which means that
`n = 3`

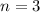
We want all red, so we find P(X = 3).

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

`P(X = 3) = h(3,11,3,7) = (C_(7,3)*C_(4,0))/(C_(11,3)) = 0.2121`

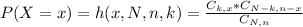
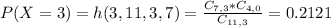
Conditional probability:

Event A: All red

Event B: From the first stack.

Probability of all red cards:

0.2121 of 50%(first stack)

1 of 50%(second stack). So

`P(A) = 0.2121*0.5 + 1*0.5 = 0.60605`

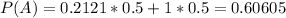
Probability of all red cards and from the first stack:

0.21 of 0.5. So

`P(A \cap B) = 0.21*0.5 = 0.105`

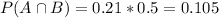
What is the probability the first stack was selected?

`P(B|A) = (P(A \cap B))/(P(A)) = (0.105)/(0.60605) = 0.1733`

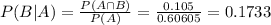
0.1733 = 17.33% probability the first stack was selected.