Answer:
There are 5,827,360 different outcomes.
Explanation:
Fundamental counting principle:
States that if there are p ways to do a thing, and q ways to do another thing, and these two things are independent, there are p*q ways to do both things.
In each party:
The order in which the people are selected is important(first is chair, second vice chair), which means that the permutations formula is used to solve this question.
Permutations formula:
The number of possible permutations of x elements from a set of n elements is given by the following formula:
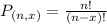
Reds:
Two from a set of 44. So
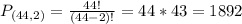
Blues:
Two from a set of 56. So
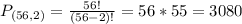
How many different outcomes are there for the chair and vice chair elections of both parties?
Considering both, by the fundamental counting principle:
1892*3080 = 5827360
There are 5,827,360 different outcomes.