A particle is moving with acceleration a ( t ) = 18 t + 16 . Its position at time t = 0 is s ( 0 ) = 10 and its velocity at time t = 0 is v ( 0 ) = 16 . What is its position at …

Question

asked Sep 5, 2022 64.8k views

1 Answer

Flaviu · Answer 1 · 2022-09-09T18:36:58+0000

Answer:

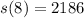
s(8)=2186

Explanation:

A particle is moving with acceleration modeled by the function:

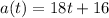
a(t)=18t+16

We are given that its position s(t) at t = 0 is 10 and that its velocity v(t) at t = 0 is 16.

And we want to find its position at t = 8.

Velocity is the integral of the acceleration. Hence:

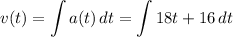
$\displaystyle v(t)=\int a(t)\, dt=\int 18t+16\, dt$

Find the velocity. Remember the constant of integration!

v(t)=9t^2+16t+C

Since v(t) is 16 when t = 0:

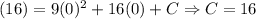
$(16)=9(0)^2+16(0)+C\Rightarrow C=16$

Hence, our velocity is given by:

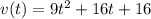
v(t)=9t^2+16t+16

Position is the integral of the velocity. Hence:

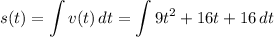
$\displaystyle s(t)=\int v(t)\, dt=\int 9t^2+16t+16\, dt$

Integrate:

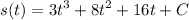
$\displaystyle s(t)=3t^3+8t^2+16t+C$

s(t) is 10 when t = 10. Hence:

C=10

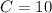
So, our position function is:

s(t)=3t^3+8t^2+16t+10

The position at t = 8 will be:

s(8)=3(8)^3+8(8)^2+16(8)+10=2186