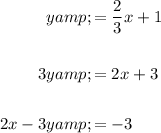Question

Find an equation of the line passing through the

point (6,5) and perpendicular to the line whose
equation is 2y + 3x = 6.

Answer 1

In slope-intercept form:

`\displaystyle y=(2)/(3)x+1`

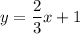
Or, in standard form:

`2x-3y=-3`

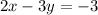
Explanation:

We want to find the equation of the line that passes through the point (6, 5) and is perpendicular to the line whose equation is:

`2y+3x=6`

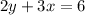
Since the new line is perpendicular, its slope and the slope of the first equation will be negative reciprocals of each other.

So, find the slope of the first equation. Subtract 3x from both sides:

`2y=-3x+6`

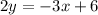
And divide both sides by two:

`\displaystyle y=-(3)/(2)x+3`

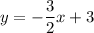
So, the slope of the first equation is -3/2.

The slope of the new line is its negative reciprocal. So, the slope of the perpendicular line is 2/3.

Next, we also know that it passes through the piont (6, 5). We can use the point-slope form:

`y-y_1=m(x-x_1)`

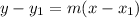
Where m is the slope and (x₁, y₁) is a point.

Substitute:

`\displaystyle y-(5)=(2)/(3)\left(x-6\right)`

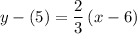
And we have our equation!

If desired, we can simplify it into slope-intercept form:

`\displaystyle \begin{aligned} y-5&=(2)/(3)x-4\\\\y&=(2)/(3)x+1\end{aligned}`

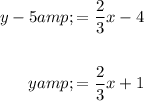
Or, into standard form:

`\displaystyle \begin{aligned} y&=(2)/(3)x+1\\\\3y&=2x+3\\\\ 2x-3y&=-3\end{aligned}`