Question

Please help!!!!

On a certain hot summer's day, 554 people used the public swimming pool. The
daily prices are $1.75 for children and $2.50 for adults. The receipts for admission totaled $1097.00.
How many children and how many adults swam at the public pool that day?

Answer 1

384 children and 170 adults

Explanation:

if x is children and y is adults

1.75x+2.5y=1097

x+y=554

1.75x=1097-2.5y

x=554-y

1.75x=1097-2.5y

1.75x=1.75(554-y)

1097-2.5y=969.5-1.75y

1097-969.5=2.5y-1.75y

127.5=0.75y

127.5/0.75=y

170=y

x+y=554

x=554-y

x=554-170

x=384

to prove these are correct just do 1.75(384)+2.5(170) and see if it equals 1097, and do 384+170 to see if its the amount of people

1.75(384)+2.5(170)

672+425

1097

384+170=554

Answer 2

Children= 384 Adults= 170

Explanation:

First, write a system of algebraic equations:

`1.75x+2.50y=1097`

`x+y=554`

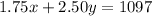
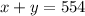
Second, use linear combination to eliminate one variable (I will eliminate x, or children.)

`1.75x+2.50y=1097`

`-1.75(x+y=554)`

`1.75x+2.50y=1097`

`-1.75x+-1.75y=-969.5`

`0.75y=127.5`

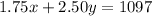
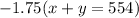
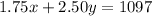
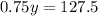
Divide both sides by 0.75

`0.75y=127.5`

`/0.75`
`/0.75`

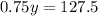
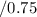
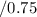
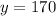`y=170`, there are 170 adults

Now, plug in 170 for
`x+y=554`

`x+170=554`

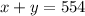
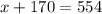
Subtract 170 from both sides

`x+170=554`

`-170`
`-170`

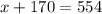
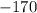
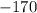
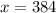`x=384`, there are 384 kids.

Hope this helps!!!