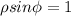Question

Name/ Uid:1. In this problem, try to write the equations of the given surface in the specified coordinates.(a) Write an equation for the sphere of radius 5 centered at the origin incylindricalcoordinates.(b) Write an equation for a cylinder of radius 1 centered at the origin and running parallel to thez-axis inspherical coordinates.

Answer 1

To find:

(a) Equation for the sphere of radius 5 centered at the origin in cylindrical coordinates

(b) Equation for a cylinder of radius 1 centered at the origin and running parallel to the z-axis in spherical coordinates

Solution:

(a) The equation of a sphere with center at (a, b, c) & having a radius 'p' is given in cartesian coordinates as:

`(x-a)^(2)+(y-b)^(2)+(z-c)^(2)=p^(2)`

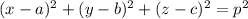
Here, it is given that the center of the sphere is at origin, i.e., at (0,0,0) & radius of the sphere is 5. That is, here we have,

`a=b=c=0,p=5`

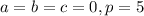
That is, the equation of the sphere in cartesian coordinates is,

`(x-0)^(2)+(y-0)^(2)+(z-0)^(2)=5^(2)`

`\Rightarrow x^(2)+y^(2)+z^(2)=25`

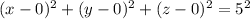
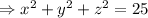
Now, the cylindrical coordinate system is represented by
`(r, \theta,z)`

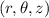
The relation between cartesian and cylindrical coordinates is given by,

`x=rcos\theta,y=rsin\theta,z=z`

`r^(2)=x^(2)+y^(2),tan\theta=(y)/(x),z=z`

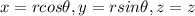
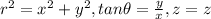
Thus, the obtained equation of the sphere in cartesian coordinates can be rewritten in cylindrical coordinates as,

`r^(2)+z^(2)=25`

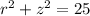
This is the required equation of the given sphere in cylindrical coordinates.

(b) A cylinder is defined by the circle that gives the top and bottom faces or alternatively, the cross section, & it's axis. A cylinder running parallel to the z-axis has an axis that is parallel to the z-axis. The equation of such a cylinder is given by the equation of the circle of cross-section with the assumption that a point in 3 dimension lying on the cylinder has 'x' & 'y' values satisfying the equation of the circle & that 'z' can be any value.

That is, in cartesian coordinates, the equation of a cylinder running parallel to the z-axis having radius 'p' with center at (a, b) is given by,

`(x-a)^(2)+(y-b)^(2)=p^(2)`

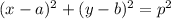
Here, it is given that the center is at origin & radius is 1. That is, here, we have,
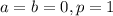`a=b=0,p=1`. Then the equation of the cylinder in cartesian coordinates is,

`x^(2)+y^(2)=1`

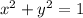
Now, the spherical coordinate system is represented by
`(\rho,\theta,\phi)`

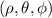
The relation between cartesian and spherical coordinates is given by,

`x=\rho sin\phi cos\theta,y=\rho sin\phi sin\theta, z= \rho cos\phi`

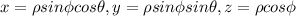
Thus, the equation of the cylinder can be rewritten in spherical coordinates as,

`(\rho sin\phi cos\theta)^(2)+(\rho sin\phi sin\theta)^(2)=1`

`\Rightarrow \rho^(2) sin^(2)\phi cos^(2)\theta+\rho^(2) sin^(2)\phi sin^(2)\theta=1`

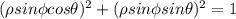
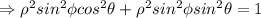
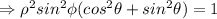
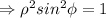`\Rightarrow \rho^(2) sin^(2)\phi (cos^(2)\theta+sin^(2)\theta)=1`

`\Rightarrow \rho^(2) sin^(2)\phi=1` (As
`sin^(2)\theta+cos^(2)\theta=1`)

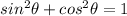Note that
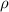`\rho` represents the distance of a point from the origin, which is always positive.
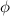`\phi` represents the angle made by the line segment joining the point with z-axis. The range of
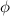`\phi` is given as
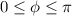`0\leq \phi\leq \pi`. We know that in this range the sine function is positive. Thus, we can say that
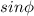`sin\phi` is always positive.

Thus, we can square root both sides and only consider the positive root as,

`\Rightarrow \rho sin\phi=1`

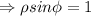
This is the required equation of the cylinder in spherical coordinates.

Final answer:

(a) The equation of the given sphere in cylindrical coordinates is
`r^(2)+z^(2)=25`

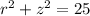
(b) The equation of the given cylinder in spherical coordinates is
`\rho sin\phi=1`