Question

A number when divided by 780 gives remainder 38 .What

reminder would be obtained by dividing same number by 26?
​

Answer 1

Given:

A number when divided by 780 gives remainder 38.

To find:

The reminder that would be obtained by dividing same number by 26.

Solution:

According to Euclis' division algorithm,

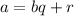`a=bq+r` ...(i)

Where, q is quotient and
`0\leq r<1` is the remainder.

It is given that a number when divided by 780 gives remainder 38.

Substituting
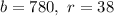`b=780,\ r=38` in (i), we get

`a=(780)q+38`

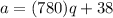
So, given number is in the form of
`780q+38`, where q is an integer.

On dividing
`780q+38` by 26, we get

`(780q+38)/(26)=(780q)/(26)+(38)/(26)`

`(780q+38)/(26)=30q+(26+12)/(26)`

`(780q+38)/(26)=30q+(26)/(26)+(12)/(26)`

`(780q+38)/(26)=30q+1+(12)/(26)`

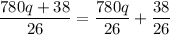
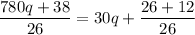
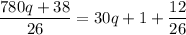
Since q is an integer, therefore (30q+1) is also an integer but
`(12)/(26)` is not an integer. Here 26 is divisor and 12 is remainder.

Therefore, the required remainder is 12.