Answer:
The 98% confidence interval to estimate the proportion of watermelon seeds that germinate is (0.4443, 0.6557). This means that we are 98% sure that the true proportion of all watermalong seeds of the company that germinate is between these two values, which means that there is good evidence that the proportion is below the 70% standard.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the z-score that has a p-value of
 .
.
Once a week for 12 weeks, he purchases a pack of 10 watermelon seeds to act as his sample. He plants the seeds in a greenhouse with good soil to maintain a consistent temperature and watering routine. He finds that the germination rate for the company's watermelon seeds is 55%.
This means that

98% confidence level
So
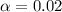 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
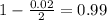 , so
, so
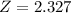 .
.
The lower limit of this interval is:

The upper limit of this interval is:
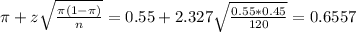
The 98% confidence interval to estimate the proportion of watermelon seeds that germinate is (0.4443, 0.6557). This means that we are 98% sure that the true proportion of all watermalong seeds of the company that germinate is between these two values, which means that there is good evidence that the proportion is below the 70% standard.