Question

A 50 kg go cart is located at the top of a 10 m tall hill….sitting motionless. It goes down the hill and rises to the top of the second hill while have a speed of 1 m/s. How tall is the second hill?

Answer 1

Step-by-step explanation:

This is a Law of Momentum Conservbation problem, where the total energy of the system cannot increase or decrease, only change form. The total energy equation for this situation is

TE = PE + KE where TE is total energy, PE is potential energy, and KE is kinetic energy. We begin by realizing that the go-kart is motionless at the top of a hill. If the kart isn't moving, then it has no KE, but if it is up off the ground and has the potential to fall to a point lower than it is curremtly, it has potential energy. That means that the total energy available to this go-kart is found in its potential energy and will not change throughout the trip's entirety. Thus,

TE = PE + 0 and

TE = (50.0)(9.8)(10.0) so

TE = 4900 J and since that's the total energy available throughout the trip, and we are looking to find the height of the next hill where this is both potential and kinetic energy, then

4900 = PE + KE and

4900 = (50.0)(9.8)(h) +
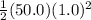`(1)/(2)(50.0)(1.0)^2` and

4900 = 490h + 25.0 and

4875 = 490h so

h = 9.9 m (I kinda ignored the rules for significant digits at the end, which goes against every teacher's bone in my body, but nonetheless, there's your answer!)