Question

A solid aluminum sphere of radius R has moment of

inertia I about an axis through its center. What is the
moment of inertia about a central axis of a solid
aluminum sphere of radius 2R?
1. 21
2. 41
3. 87
4. 161
5. 321​

Answer 1

5. 32I

Step-by-step explanation:

The moment of inertia of a solid sphere about its central axis is given by

I =
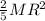`(2)/(5) MR^2` ------------------(i)

Where;

M = mass of the sphere

R = radius of the sphere.

From the question;

Case 1: The aluminum sphere has a radius R and moment of inertia I.

This means that we can substitute these values of R and I into equation (i) and get;

I =
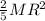`(2)/(5) MR^2` --------------(ii)

M is the mass of the aluminum sphere and is given by;

M = pV

Where;

p = density of aluminum

V = Volume of the sphere =
`(4)/(3) \pi R^3`

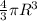
=> M = p(
`(4)/(3) \pi R^3`) --------------------(*)

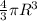Case 2: An aluminum sphere with a radius of 2R instead.

Let the moment of inertia in this case be I' and mass be M'

Substituting R = 2R, M = M' and I = I' into equation (i) gives

I' =
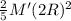`(2)/(5) M'(2R)^2` ------------------(iii)

Where;

M' = pV'

p = density of aluminum

V' = volume of the sphere =
`(4)/(3) \pi (2R)^3`

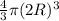
=> M' = p(
`(4)/(3) \pi (2R)^3`)

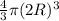Rewriting gives;

M' = p(
`(4)/(3) \pi (2)^3(R)^3`)

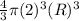M' = p(
`(4)/(3) \pi8(R)^3`)

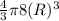M' = 8p(
`(4)/(3) \pi R^3`)

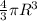From equation (*), this can be written as

M' = 8M

Now substitute all necessary values into equation (ii)

I' =
`(2)/(5) M'(2R)^2`

I' =
`(2)/(5) (8M)(2R)^2`

I' =
`(2)/(5) (8M)(2)^2(R)^2`

I' =
`(2)/(5) (8M)(4)(R)^2`

I' =
`(2)/(5) (32M)(R)^2`

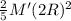
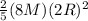
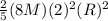
I' =
`32[(2)/(5)MR^2]`

Comparing with equation (ii)

I' =
`32[I]`

Therefore, the moment of inertia about a central axis of a solid

aluminum sphere of radius 2R is 32I