Question

An express train travel from A to B for 4 hours. A normal train travel from B to A for 10 hours. Both of them started at the same time. The average speed of the express train is greater than the average speed of the normal train 90km/h. Find the average speed of the normal train?

Answer 1

The speed of the normal train is 60 kilometers per hour.

Explanation:

Let suppose that both trains move at constant speed and cover the same distance. Then, we have the following identity:

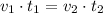`v_(1)\cdot t_(1) = v_(2)\cdot t_(2)` (1)

Where:

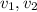`v_(1), v_(2)` - Average speeds of the express train and the normal train, in kilometers per hour.

`t_(1), t_(2)` - Travel times of the express train and the normal train, in hours.

In addition, there is the following relationship between average speeds:

`v_(1) = v_(2) + 90` (2)

By (2) in (1), we have the following expression for the average speed of the normal train:

`(v_(2) + 90) \cdot t_(1) = v_(2)\cdot t_(2)`

`90\cdot t_(1) = v_(2) \cdot (t_(2) - t_(1))`

`v_(2) = (90\cdot t_(1))/(t_(2)-t_(1))`

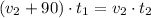
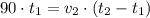
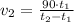
If we know that
`t_(1) = 4\,h` and
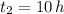`t_(2) = 10\,h`, then the average speed of the normal train is:

`v_(2) = 90\cdot \left((4\,h)/(10\,h - 4\,h) \right)`

`v_(2) = 60\,(km)/(h)`

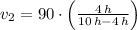
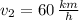
The speed of the normal train is 60 kilometers per hour.