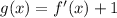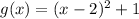Answer:
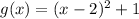
Explanation:
Given
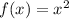
Required
Determine g(x)
f(x) represents the parent function. And from the graph, we have:
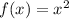
f(x) is first shifted 2 units right.
The rule is:
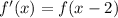
So, we have:
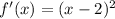
Next, f'(x) is shifted 1 unit up to give g(x), the blue graph.
The rule to this is: