Question

How do you find the amplitude, period, and shift for f(x)=−4cos(3x−π)+1?

Answer 1

(a) Amplitude = 4

(b)
`T = (2\pi)/(3)` --- Period

(c)

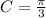`C = (\pi)/(3)` --- phase shift

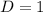`D =1` --- vertical shift

Explanation:

Given

`f(x) = -4\cos(3x - \pi) + 1`

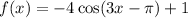
Rewrite the function as:

`f(x) = -4\cos(3(x - (\pi)/(3)) + 1`

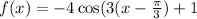
Solving (a): The amplitude

A cosine function is represented as:

`f(x) = A\cos[B(x - C)] + D`

Where:

`|A| \to Amplitude`

So, in this equation (by comparison):

`|A| = |-4|`

`|A| = 4`

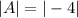
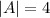
The amplitude is 4

Solving (b): The period (T)

This is calculated as:

`T = (2\pi)/(B)`

By comparison:

`B =3`

So:

`T = (2\pi)/(3)`

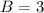
Solving (c): The shift

The phase shift is C

The vertical shift is D

By comparison:

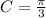`C = (\pi)/(3)` --- phase shift

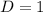`D =1` --- vertical shift