Question

Find the equation for the

following parabola.
Vertex (-2,-4)
Focus (-4,-4)
A. (7-4)2 = -8(x-2)
B. (x+4)2 = 8(y+2)
C. (y+4)2 = 8(x+2)
D. (y+4)2 = -8(x+2)

Answer 1

(y+4)2=−8(x+2)

The answer would be D.

Answer 2

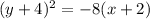`(y+4)^2 = -8(x+2)`, option D.

Explanation:

Equation of a parabola:

The equation of a parabola has the following format:

`(y - k)^2 = 4p(x-h)`

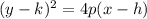
In which the center is (h,k) and the focus is (h+p,k).

Vertex (-2,-4)

This means that
`h = -2, k = -4`

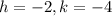
So

`(y - k)^2 = 4p(x-h)`

`(y - (-4))^2 = 4p(x-(-2))`

`(y+4)^2 = 4p(x+2)`

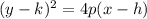
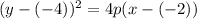
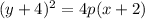
Vertex (-2,-4)

Focus (-4,-4)

-4 - (-2) = -4 + 2 = -2

So p = -2 and

`(y+4)^2 = 4(-2)(x+2)`

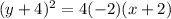
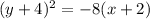`(y+4)^2 = -8(x+2)`, option D.