Question

Help find average rate of change

Answer 1

Problem 2

Answer: Average rate of change = 4

==========================================================

Step-by-step explanation:

When we have an interval [a,b], the average rate of change over this interval is given by the formula

`m = (f(b)-f(a))/(b-a)`

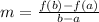
You probably can notice that we have something that looks eerily similar to the slope formula. That's because average rates of change are basically the same as the slope of the straight line through the endpoints of the interval. The f(b)-f(a) is the change in y of f(x) outputs. The b-a down below is the change of x values when going from x = a to x = b.

-------------------

Let's evaluate the function at x = 1

f(x) = x^2+1

f(1) = 1^2+1

f(1) = 2

Repeat for x = 3

f(x) = x^2+1

f(3) = 3^2+1

f(3) = 10

--------------------

We have enough info to evaluate the original formula I mentioned earlier

`m = (f(b)-f(a))/(b-a)\\\\m = (f(3)-f(1))/(3-1)\\\\m = (10-2)/(3-1)\\\\m = (8)/(2)\\\\m = 4\\\\`

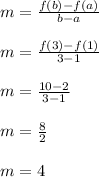
The average rate of change on this interval is 4

This is the same as saying the slope of the line through (1,2) and (3,10) is m = 4

See the graph below.