2 Answers

Mmachenry · Answer 1 · 2022-07-04T20:02:09+0000

Answer:

It will take 25.6 years for the mass of the sample to reach 400 grams.

Explanation:

Element X is a radioactive isotope such that every 25 years, its mass decreases by half.

This means that the amount of the substance after t years can be modeled by a function in the following format:

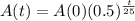
$A(t) = A(0)(0.5)^{(t)/(25)}$

In which A(0) is the initial amount.

Initial mass of a sample of Element X is 910 grams.

This means that
A(0) = 910

So

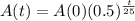
$A(t) = A(0)(0.5)^{(t)/(25)}$

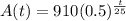
$A(t) = 910(0.5)^{(t)/(25)}$

How long would it be until the mass of the sample reached 400 grams?

This is t for which
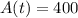
A(t) = 400

So

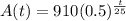
$A(t) = 910(0.5)^{(t)/(25)}$

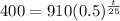
$400 = 910(0.5)^{(t)/(25)}$

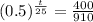
$(0.5)^{(t)/(25)} = (400)/(910)$

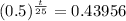
$(0.5)^{(t)/(25)} = 0.43956$

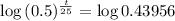
$\log{(0.5)^{(t)/(25)}} = \log{0.43956}$

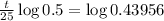
$(t)/(25)\log{0.5} = \log{0.43956}$

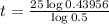
$t = \frac{25\log{0.43956}}{\log{0.5}}$

t = 25.6

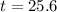
It will take 25.6 years for the mass of the sample to reach 400 grams.

Please log in or register to add a comment.