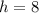1 Answer

Luan Fonseca · Answer 1 · 2022-04-10T23:30:50+0000

Answer:

The height is 8cm

Explanation:

Given

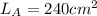L_A = 240cm^2 --- lateral area

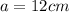a = 12cm --- base lengths

Required

The height of the pyramid

The lateral area of a square pyramid is:

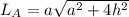
$L_A = a\sqrt{a^2 + 4h^2$

So, we have:

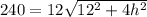
$240 = 12\sqrt{12^2 + 4h^2$

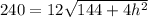
$240 = 12\sqrt{144 + 4h^2$

Divide both sides by 12

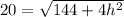
$20 = \sqrt{144 + 4h^2$

Square both sides

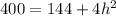
400 = 144 + 4h^2

Collect like terms

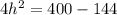
4h^2 = 400 - 144

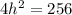
4h^2 = 256

Divide by 4

h^2 = 64

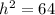
Take square roots

h = 8

Please log in or register to add a comment.