A book that is 13 inches tall is leaning against the edge of a wall. If the bottom of the book is 5 inches from the wall, how far up the wall is the top of the book?

Question

asked Feb 13, 2022 59.7k views

1 Answer

Alexander Beninski · Answer 1 · 2022-02-17T03:58:17+0000

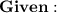
$\huge\bold{Given:}$

Length of the book (hypotenuse) = 13 inches

Distance of the book from the foot of the wall (base) = 5 inches

$\huge\bold{To\:find:}$

Length of the book on the wall (perpendicular ''
").

$\large\mathfrak{{\pmb{\underline{\orange{Solution}}{\orange{:}}}}}$

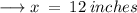
$\longrightarrow{\purple{x\:=\:12\:inches}}$

$\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\red{:}}}}}$

By Pythagoras theorem, we have

(Perpendicular)² + (Base)² = (Hypotenuse)²

$\longrightarrow{\blue{}}$
${x}^(2)$ + (5 in) ² = (13 in)²

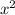$\longrightarrow{\blue{}}$
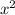${x}^(2)$ + 25 in² = 169 in²

$\longrightarrow{\blue{}}$
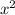${x}^(2)$ = 169 in² - 25 in²

$\longrightarrow{\blue{}}$
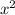${x}^(2)$ = 144 in²

$\longrightarrow{\blue{}}$
=
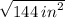
$\sqrt{144 \: {in}^(2) }$

$\longrightarrow{\blue{}}$
=
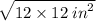
$\sqrt{12 * 12 \: {in}^(2) }$

$\longrightarrow{\blue{}}$
=
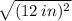
$\sqrt{ ({12 \: in})^(2) }$

$\longrightarrow{\blue{}}$
= 12 in

Therefore, the height of the book on the wall
is 12 inches.

$\huge{\textbf{\textsf{{\orange{My}}{\blue{st}}{\pink{iq}}{\purple{ue}}{\red{35}}{\green{☂}}}}}$