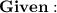
Length of the perpendicular = 6 ft.
Length of the base = 8 ft.
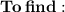
The length of the missing side.

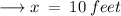
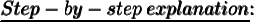
Let
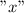 be the side of the hypotenuse.
be the side of the hypotenuse.
Using Pythagoras theorem, we have
( Hypotenuse )² = ( Perpendicular )² + ( Base )²

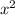 = ( 6 ft )² + ( 8 ft) ²
= ( 6 ft )² + ( 8 ft) ²

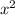 = 36 ft² + 64 ft²
= 36 ft² + 64 ft²

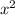 = 100 ft²
= 100 ft²

 =
=
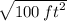

 =
=
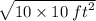

 =
=
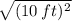

 = 10 ft.
= 10 ft.
Therefore, the length of the missing side
 is 10 feet.
is 10 feet.
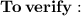
 ( 10 ft )² = ( 6 ft )² + ( 8 ft ) ²
( 10 ft )² = ( 6 ft )² + ( 8 ft ) ²
 100 ft² = 36 ft² + 64 ft²
100 ft² = 36 ft² + 64 ft²
 100 ft² = 100 ft²
100 ft² = 100 ft²
 L.H.S. = R. H. S.
L.H.S. = R. H. S.
Hence verified. ✔