Question

The table represents an exponential function.

What is the multiplicative rate of change of the
function?
Х
1
3
.
2.
4
9
16
9

Answer 1

Explanation:

An exponential function has a standard form

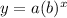`y=a(b)^x` where a is the initial value, b is the rate of growth or decay, and x and y are found in coordinates from the table. We need to solve for b, the rate of change (growth or decay). We will use the first 2 coordinates in the table, namely (1, 6) and (2, 4) to solve for b. We will use a system of equations...2 equations for 2 unknowns. The first equation is found by plugging in a 6 for y and a 1 for x to get:

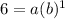`6=a(b)^1` and, solved for a:

`a=(6)/(b)`.

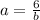In the second equation, we will plug in a 4 for y, a 2 for x and the value for a we just found:

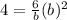`4=(6)/(b)(b)^2` and, simplified a bit:

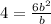`4=(6b^2)/(b)` which finally simplifies to

4 = 6b and

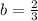`b=(2)/(3)`. That's the rate of change we are asked to find. We could continue to find the whole equation. Plug in 2/3 for b to solve for a:

`a=(6)/((2)/(3) )` and

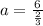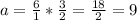`a=(6)/(1)*(3)/(2)=(18)/(2)=9` and the exponential equation is

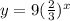`y=9((2)/(3))^x` that means that we started with 9 of something and it is dying/decaying/depreciating at a rate of 33%