Question

Use the equation
`A=Pe^r^t` where P represents the principall amount, t represents time and r is the interest rate.

Question 1
Suppose you deposit $3000 in an account paying 2% annual interest compounded continuously. Find the balance (A) after 5 years.
Balance _____ (2 places)
How long will iot take before you have $5000 in your account? _____ (1 place)

Question 2
Suppose you deposit $100 in an account paying 3.5% annual interest compounded continuously.

How long will it take to double your money? _____ (1 place)
What interest rate would you need in order to have $300 after 10 years? _____ (1 place)

Answer 1

9514 1404 393

Answer:

1. $3,315.51; 25.5 years
2. 19.8 years; 11.0%

Explanation:

The questions involve using the formula to find values of A, t, and r. The formula already gives A. We can solve it for t and r:

`A=Pe^(rt)\\\\ ln((A))=ln((P))+rt\qquad\text{take natural logs}\\\\t=(ln((A))-ln((P)))/(r)\qquad\text{solve for t}\\\\r=(ln((A))-ln((P)))/(t)\qquad\text{solve for r}`

__

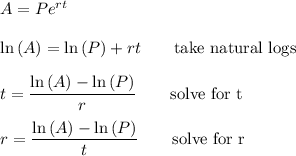
1a.

P=$3000, r=0.02, t=5

A = $3000e^(.02·5) ≈ $3315.51

__

1b.

P=$3000, A=$5000, r=0.02

t = (ln(5000) -ln(3000)/0.02 ≈ 25.5 . . . years

__

2a.

P=$100, r=0.035, A=$200

t = (ln(200) -ln(100))/0.035 ≈ 19.8 . . . years

__

2b.

P=$100, A=$300, t=10

r = (ln(300) -ln(100))/10 ≈ 0.10986 ≈ 11.0%

_____

Additional comment

Of course, ln(A) -ln(P) = ln(A/P). Here, the fraction A/P is found easily using mental arithmetic, so this simplification can save a step in the calculation of time or rate.