
Given :-
- Here, we have composite figure which is composed of 2 cuboids.
- The dimensions of larger cuboid is 12cm, 7cm, 7cm
- The dimensions of smaller cuboid is 7cm, 2cm , 2cm
To Find :-
- We have to find the total surface area of the composite figure
Let's Begin :-
Here,
The dimension of larger cuboid are
- Length = 12cm
- Breath = 7 cm
- height = 7 cm
We know that,
Lateral surface area of cuboid
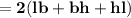
Subsitute the required values,
![\sf{ = 2[(7)(7) + (7)(12) +(7)(12) ]}](https://img.qammunity.org/2023/formulas/mathematics/college/dbvuqvympmglknww6ifz9yuuw4ygfu1ozv.png)
![\sf{ = 2[ 49 + 84 ]}](https://img.qammunity.org/2023/formulas/mathematics/college/xs8krmlstjtei9woboqbow2i6d77d8cw6l.png)
![\sf{ = 2[ 49 + 168 ]}](https://img.qammunity.org/2023/formulas/mathematics/college/rbwk8ii2pu2qsqvyyjbgg1w526o9cx4r2d.png)
![\sf{ = 2[ 217 ]}](https://img.qammunity.org/2023/formulas/mathematics/college/k48i1mvf0endn9uzbunbewqyt9dew4up0q.png)
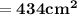
Now,
We have to find the lateral surface area of smaller cuboid
- The dimensions of smaller cuboid are 7cm, 2cm and 2cm
Therefore,
Lateral surface area of smaller cuboid
![\sf{ = 2[(2)(7) + (7)(2) +(2)(2) ]}](https://img.qammunity.org/2023/formulas/mathematics/college/v5g25vr1pse1vgis15yk0u2ynvhvgqg5wx.png)
![\sf{ = 2[ 14 + 14 + 4 ]}](https://img.qammunity.org/2023/formulas/mathematics/college/9jq9nwf9ohleh09q5gr1ec39rstca6yoy1.png)
![\sf{ = 2[ 28 + 4 ]}](https://img.qammunity.org/2023/formulas/mathematics/college/wxtbd2wy4mu1cqhcde8v7oizzi2u0pcjzj.png)
![\sf{ = 2[ 32]}](https://img.qammunity.org/2023/formulas/mathematics/college/1gfxqyygepb6y5h2sfebalextaz8zdt5me.png)
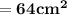
The common base area of both the cuboids
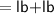
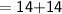
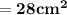
Now,
The total surface area of the given composite figure
= SA of larger cuboid + SA of smaller cuboid - common base area
Subsitute the required values,
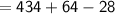
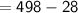
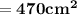
Hence, The surface area of composite figure is 470 cm² .