Question

What is the equation of the parabola with focus (-1/4,-2/3) and directrix y=3/4?

A. y = -x^2 +8x -7
B. y = -1/2x^2 +14/5x +17/53
C. y = -6/17x^2 - 3/17x +1/51
D. y = -1/6x^2

Answer 1

Given:

Focus of the parabola =
`\left(-(1)/(4),-(2)/(3)\right)`

Directrix of the parabola is
`y=(3)/(4)`.

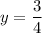To find:

The equation of the parabola.

Solution:

The equation of the parabola is:

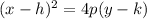`(x-h)^2=4p(y-k)` ...(i)

Where, (h,k) is vertex, (h,k+p) is focus and
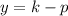`y=k-p` is the directrix.

It is given that the focus of the parabola is at
.

`(h,k+p)=\left(-(1)/(4),-(2)/(3)\right)`

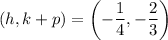
On comparing both sides, we get

`h=-(1)/(4)`

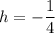
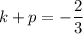`k+p=-(2)/(3)` ...(ii)

Directrix of the parabola is
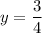`y=(3)/(4)`. So,

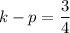`k-p=(3)/(4)` ...(iii)

Adding (ii) and (iii), we get

`2k=-(2)/(3)+(3)/(4)`

`2k=(-8+9)/(12)`

`k=(1)/(12* 2)`

`k=(1)/(24)`

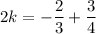
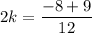
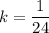
Putting
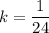`k=(1)/(24)` in (ii), we get

`(1)/(24)+p=-(2)/(3)`

`p=-(2)/(3)-(1)/(24)`

`p=(-16-1)/(24)`

`p=(-17)/(24)`

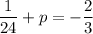
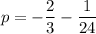
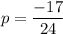
Putting
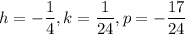`h=-(1)/(4),k=(1)/(24), p=-(17)/(24)` in (i), we get

`\left(x-(-(1)/(4))\right)^2=4\left(-(17)/(24)\right)\left(y-(1)/(24)\right)`

`\left(x+(1)/(4)\right)^2=-(17)/(6)\left(y-(1)/(24)\right)`

`x^2+2(x)((1)/(4))+((1)/(4))^2=-(17)/(6)\left(y-(1)/(24)\right)`

`-(6)/(17)\left(x^2+(1)/(2)x+(1)/(16)\right)=y-(1)/(24)`

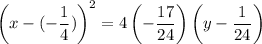
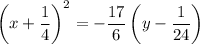
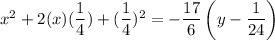
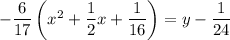
On further simplification, we get

`-(6)/(17)(x^2)-(6)/(17)((1)/(2)x)-(6)/(17)((1)/(16))=y-(1)/(24)`

`-(6)/(17)x^2-(3)/(17)x-(3)/(136)+(1)/(24)=y`

`-(6)/(17)x^2-(3)/(17)x+(-9+17)/(408)=y`

`-(6)/(17)x^2-(3)/(17)x+(8)/(408)=y`

`-(6)/(17)x^2-(3)/(17)x+(1)/(51)=y`

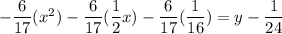
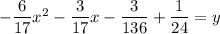
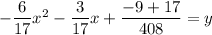
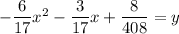
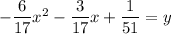
Therefore, the equation of the parabola is
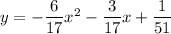`y=-(6)/(17)x^2-(3)/(17)x+(1)/(51)`. Hence, the correct option is C.