Answer:
The height of the tree is 6.12 meters and the height of the building is 33.12 meters.
Explanation:
Since the person is 1.8 meters tall, HC = 1.8
And since their shadow is 10 meters long, HD = 10.
We are also given that GH is 24 meters and that FG is 150 meters.
Height of the Tree:
The height of the tree is given by GB.
Again, since m∠BGD = m∠CHD = 90°, ∠BGD ≅ ∠CHD.
Likewise, ∠D ≅ ∠D. So, by AA-Similarity:
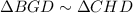
Corresponding parts of similar triangles are in proportion. Therefore:

Note that:
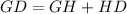
Find GD:

Substitute the known values into the proportion:
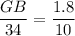
Cross-multiply:
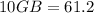
Therefore:
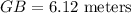
The height of the tree is 6.12 meters.
Height of the Building:
The height of the building is given by FA.
Since m∠AFD = m∠CHD = 90°, ∠AFD ≅ ∠CHD.
∠D ≅ ∠D. So, by AA-Similarity:
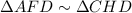
Corresponding parts of similar triangles are in proportion. Therefore:

Note that:
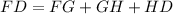
Find FD:

Substitute the known values into the proportion:
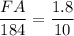
Cross-multiply:
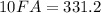
Therefore:
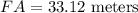
The height of the building is 33.12 meters.