Question

The function f(x) = –x2 – 4x + 5 is shown on the graph. On a coordinate plane, a parabola opens down. It goes through (negative 5, 0), has a vertex at (negative 2, 9), and goes through (1, 0). Which statement about the function is true? The domain of the function is all real numbers less than or equal to −2. The domain of the function is all real numbers less than or equal to 9. The range of the function is all real numbers less than or equal to −2. The range of the function is all real numbers less than or equal to 9.

Answer 1

D

Explanation:

We have the quadratic function:

`f(x)=-x^2-4x+5`

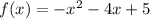
First, the domain of all quadratics is always all real numbers unless otherwise specified. You can let x be any number and the function will be defined.

So, we can eliminate choices A and B.

Note that since the leading coefficient is negative, the parabola will be curved downwards. Therefore, it will have a maximum value. This maximum value is determined by its vertex, which is (-2, 9).

Since it is curving downwards, the maximum value of the parabola is y = 9. It will never exceed this value. Therefore, the range or the set of y-value possible is always equal to or less than 9.

So, the range of the function is all real numbers less than or equal to 9.

Our answer is D.

It is not C because the maximum value is dependent on y and not x.