Question

(03.01 LC)

Which of the following is equal to √3√2? (4 points)

Answer 1

The answer is
`2^{(1)/(6) }`.

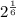Explanation:

To find which answer is equal to
`\sqrt{} \sqrt[3]{2}`, start by simplifying
`\sqrt{} \sqrt[3]{2}`. The radical will simplify to
`\sqrt[6]{2}`.

An easy way to determine which answer is correct, convert each of the numbers to decimal form.

For
`\sqrt[6]{2}`, it will look like 1.122 in decimal form.

For
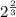`2^{(2)/(3) }`, it will look like 1.587 in decimal form.

For
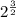`2^{(3)/(2) }`, it will look like 2.828 in decimal form.

For
`2^{(1)/(3) }`, it will look like 1.260 in decimal form.

For
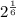`2^{(1)/(6) }`, it will look like 1.122 in decimal form.

Then, by seeing which two decimal forms are the same, it causes the answer to be
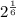`2^{(1)/(6) }`.

Answer 2

D

Explanation:

We are given:

`\displaystyle \sqrt{\sqrt[3]{2}}`

Recall the property:

`\displaystyle \sqrt[b]{x}=x^(1/b)`

Hence:

`\displaystyle \sqrt{\sqrt[3]{2}}=\sqrt{2^(1/3)}`

Using the same property:

`\sqrt{2^(1/3)}=(2^(1/3))^(1/2)`

Recall the property:

`(x^a)^b=x^(ab)`

Hence, multiply:

`(2^(1/3))^(1/2)=2^(1/6)`

Therefore:

`\displaystyle \sqrt{\sqrt[3]{2}}=2^(1/6)`

Our answer is D.