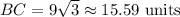Question

Can someone answer with steps and explanation? Thanks.

Answer 1

`BC=9√(3)\approx15.59\text{ units}`

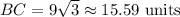
Explanation:

Since Segment BOA is a diameter:

`m\angle ACB=90`

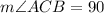
Arc Ac and Arc CB are in a ratio of two to four. Since Segment BOA is a diameter, Arc ACB measures 180°. Letting the unknown value be x, we can write that:

`2x+4x=180`

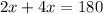
Hence:

`x=30`

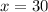
Thus, Arc CB = 120°. By the Inscribed Angle Theorem:

`\displaystyle m\angle A=(1)/(2)\left(\stackrel{\frown}{CB}\right)=(1)/(2)\left(120)=60`

Therefore, ΔABC is a 30-60-90 triangle. Its sides are in the ratios shown in the image below.

Since AC is opposite from the 30° triangle, let AC = a.

We are given that AC = 9. Hence, a = 9.

BC is opposite from the 60° angle and it is given by a√3. Therefore:

`BC=9√(3)\approx15.59\text{ units}`