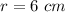Answer:
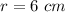
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Geometry
Volume of a Cone Formula:
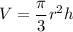
Explanation:
Step 1: Define
Identify variables
V = 120π cm³
h = 10 cm
Step 2: Solve for r
- Substitute in variables [Volume of a Cone Formula]:
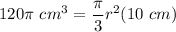
- Multiply:
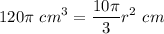
- [Division Property of Equality] Divide
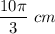 on both sides:
on both sides:
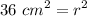
- [Equality Property] Square root both sides:
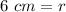
- Rewrite: