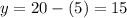Question

Need Help ASAP! Timed Assignment!

Mike and his friends bought cheese wafers for $2 per packet and chocolate wafers for $1 per packet at a carnival. They spent a total of $25 to buy a total of 20 packets of wafers of the two varieties.

Part A: Write a system of equations that can be solved to find the number of packets of cheese wafers and the number of packets of chocolate wafers that Mike and his friends bought at the carnival. Define the variables used in the equations. (5 points)

Part B: How many packets of chocolate wafers and cheese wafers did they buy? Explain how you got the answer and why you selected a particular method to get the answer. (5 points)

Answer 1

Part A)

Our system of equation is:

`\displaystyle \begin{aligned} 2x+y&=25\\x+y&=20\end{aligned}`

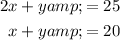
Where x represent the amount of cheese wafers bought and y represent the amount of chocolate wafers bought.

Part B)

Mike and his friends bought five cheese wafers and 15 chocolate wafers.

Explanation:

Let cheese wafers be represented by x and let chocolate wafers be represented by y.

Part A)

They spent a total of $25. Since each cheese wafer cost $2 and each chocolate wafer cost $1, we can write that:

`2x+1y=25`

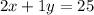
Or, simply:

`2x+y=25`

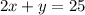
They also purchased a total of 20 packets of wafers. Hence:

`x+y=20`

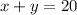
Our system of equation is:

`\displaystyle \begin{aligned} 2x+y&=25\\x+y&=20\end{aligned}`

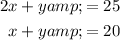
Where x represent the amount of cheese wafers bought and y represent the amount of chocolate wafers bought.

Part B)

Since both equations have the same coefficient for y, we can use elimination. First, multiply the second equation by negative one:

`-x-y=-20`

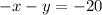
Add it to the first equation:

`(2x+y)+(-x-y)=(25)+(-20)`

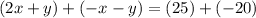
Simplify:

`x=5`

So, five cheese wafers were bought.

Using the second equation again, we can see that:

`(5)+y=20\Rightarrow y=15`

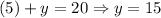
So, 15 chocolate wafers were bought.

Notes:

If we wanted to solve this using substitution, we can subtract x (or y, doesn't really matter) from both sides from either equation. Using the second equation, this yields:

`y=20-x`

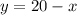
Substitute this into the first:

`2x+(20-x)=25`

Simplify:

`x=5`

And we will acquire the same answer:

`y=20-(5)=15`