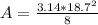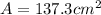Question

6. a semicircle has as its diameter the hypotenuse of a right triangle shown below. determine the area of the semicircle to the nearest tenth of a square centimeter. show how you arrived at your answer.

Answer 1

`A = 137.3cm^2`

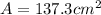
Explanation:

Given

See attachment

Required

The area of the semicircle

First, we calculate the hypotenuse (h) of the triangle

Considering only the triangle, we have:

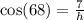`\cos(68) = (7)/(h)` --- cosine formula

Make h the subject

`h = (7)/(\cos(68))`

`h = (7)/(0.3746)`

`h = 18.7`

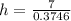
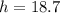
The area of the semicircle is then calculated as:

`A = (\pi h^2)/(8)`

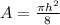
This gives:

`A = (3.14 * 18.7^2)/(8)`

`A = (1098.03)/(8)`

`A = 137.3cm^2`