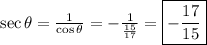Question

If sin theta = 8/17 and cot theta < 0, what is sec theta?

Answer 1

`-(17)/(15)`

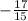
Explanation:

By definition,
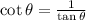`\cot \theta=(1)/(\tan \theta)` and
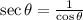`\sec \theta=(1)/(\cos \theta)`. Since since
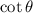`\cot \theta` is negative,
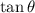`\tan \theta` must also be negative, and since
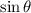`\sin \theta` is positive, we must be in Quadrant II.

In a right triangle, the sine of an angle is equal to its opposite side divided by the hypotenuse. The cosine of an angle in a right triangle is equal to its adjacent side divided by the hypotenuse. Therefore, we can draw a right triangle in Quadrant II, where the opposite side to angle theta is 8 and the hypotenuse of the triangle is 17.

To find the remaining leg, use to the Pythagorean Theorem, where
`a^2+b^2=c^2`, where
`c` is the hypotenuse, or longest side, of the right triangle and
`a` and
`b` are the two legs of the right triangle.

Solving, we get:

`8^2+b^2=17^2,\\b^2=17^2-8^2,\\b^2=√(17^2-8^2)=√(225)=15`

Since all values of cosine theta are negative in Quadrant II, all values of secant theta must also be negative in Quadrant II.

Thus, we have:

`\sec\theta=(1)/(\cos \theta)=-(1)/((15)/(17))=\boxed{-(17)/(15)}`