Question

2x to the power of -2
the answer is apparently 2 over x squared
explain this

Answer 1

See Below

Explanation:

When you have a negative exponent, you divide by the exponent hence the flipping. Here is an example to make it easier to explain. Below are some power of ten:

`10^3=1000\\10^2=100\\10^1=10\\10^0 =1\\10^(-1)=(1)/(10) =(1)/(10^1) \\10^(-2)=(1)/(100) =(1)/(10^2)`

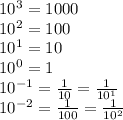
When you go from an exponent to the one below it, you divide by the base. For example, to go from
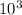`10^3` to
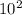`10^2`, you divide by ten. This is the same principle used to find the values of negative exponents.
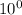`10^0` is
`10^1` divided by 10, so
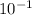`10^(-1)` should be
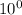`10^0` divided by ten.
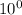`10^0` is 1, making the value of
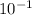`10^(-1)` as
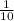`(1)/(10)`. When you divide by ten, you multiply by
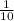`(1)/(10)`, this effect makes the exponent stack on the bottom and correspond to the magnitude of the power.

For this specific example, we can write:

`2x^(-2)`

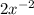
We are raising x to the power of negative 2, so we can say it is the same as
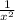`(1)/(x^2)`. We are also multiplying by 2, so that's how we get
`(2)/(x^2)`

If you need more of a visual, here are the powers of x:

`x^2\\x^1=(x^2)/(x) \\x^0=(x^1)/(x)=1 \\x^(-1)=(1)/(x) \\x^(-2)=(x^(-1))/(x)=(1)/(x*x)=(1)/(x^2)`

And we just multiply 2 times the value of
`x^(-2)`.

Hope this helps.