Question

The base of a solid is a circular disk with radius 4. Parallel cross sections perpendicular to the base are squares. Find the volume of the solid.

Answer 1

the volume of the solid is 1024/3 cubic unit

Explanation:

Given the data in the question,

radius of the circular disk = 4

Now if the center is at ( 0,0 ), the equation of the circle will be;

x² + y² = 4²

x² + y² = 16

we solve for y

y² = 16 - x²

y = ±√( 16 - x² )

{ positive is for the top while the negative is for the bottom position }

A = b²

b = 2√( 16 - x² ) { parallel cross section }

A = [2√( 16 - x² )]²

A = 4( 16 - x² )

Now,

VOLUME =
`\int\limits^r -rA dx`

=
`\int\limits^4_4 {-4(16-x^2)} \, dx`

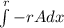
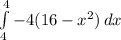
= 4[ 16x - (x³)/3 ] { from -4 to 4 }

= 4[ ( 64 - 64/3 ) - (-64 = 64/3 0 ]

= 4[ 64 - 64/3 + 64 - 64/3 ]

= 4[ (192 - 64 + 192 - 64 ) / 3 ]

= 4[ 256 / 3 ]

= 1024/3 cubic unit

Therefore, the volume of the solid is 1024/3 cubic unit