Question

The annual commissions per salesperson employed by a manufacturer of light machinery averaged $40,000 with a standard deviation of $5,000. What percent of the sales persons earn between $32,000 and $42,000?

A) 60.06%.
B) 39.94%.
C) 34.13%.
D) 81.66%.

Answer 1

A

Step-by-step explanation:

From the given information;

The required probability needed to carry out is P(32000<X<42000);

Given that:

mean
`\mu` = 40000

standard deviation
`\sigma` = 5000

Using the standard normal distribution;

`P(32000 <X<42000) = ( (x - \mu)/(\sigma) <Z< (x - \mu)/(\sigma))`

`P(32000 <X<42000) = ( (32000 - 40000)/(5000) <Z< (42000 - 40000)/(5000))`

`P(32000 <X<42000) = ( -1.6<Z<0.4)`

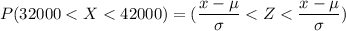
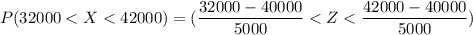
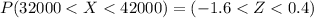
Here, the region of the area lies between -1.60 and 0.40

∴

P(320000 < X < 40000) = P(Z<0.40) - P(Z< -0.40)

From Z tables;

P(320000 < X < 40000) = 0.6554 -0.0548

P(320000 < X < 40000) = 0.6006

P(320000 < X < 40000) = 60.06%