Question

The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widget weights have a mean of 42 ounces and a standard deviation of 10 ounces. Use the Empirical Rule.

a. 99.7% of the widget weights lie between _____ and _____.
b. What percentage of the widget weights lie between 26 and 66 ounces?
c. What percentage of the widget weights lie above 34?

Answer 1

The answer is below

Explanation:

The empirical rule states for a normal distribution, 68% of the data falls within one standard deviation, 95% falls within two standard deviations and 99.7% falls within three standard deviations.

z score is given by:

`z=(x-\mu)/(\sigma)`

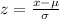
Given that mean (μ) = 42 ounces, standard deviation (σ) = 10 ounces.

a) 99.7% falls within three standard deviations. Therefore:

99.7% falls within μ ± 3σ = 42 ± 3(10) = 42 ± 30 = (12, 72)

Therefore 99.7% falls within 12 ounce and 72 ounce.

b) For x > 26

`z=(26-42)/(10)=-1.6\\`

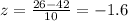
For x < 66

`z=(66-42)/(10)=2.4\\`

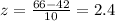
From the normal distribution table, P(26 < x < 66) = P(-1.6 < z < 2.4) = P(z < 2.4) - P(z < -1.6) = 0.9918 - 0.0548 = 0.937 = 93.7%

c) For x > 34

`z=(34-42)/(10)=-0.8\\`

From the normal distribution table, P(x > 34) = P(z > -0.8) = 1 - P(z < -0.8) = 1 - 0.2119 = 0.7881 = 78.81%

Answer 2

Explanation:

Given that:

Mean
`\mu` = 42

standard deviation
`\sigma` = 10

Using Empirical Rule:

`\mu` -
`\sigma` = 42 - 10 = 32
`\mu` +
`\sigma` = 42 + 10 = 52

`\mu` - 2
`\sigma` = 42 - 2(10) = 22
`\mu` + 2
`\sigma` = 42 + 2(10) = 62

`\mu` - 3
`\sigma` = 42 - 3(10) = 12
`\mu` + 3
`\sigma` = 42 + 3(10) = 72

The curve is attached in the image below.

a). the widget of 99.7% lies between 12 and 72

b) 68 + 13.5 = 81.5%

c) 50 + 34 = 84%