Answer:
0.73 = 73% probability that a randomly selected student is either male or would admit to lying to a teacher, during the past year.
Explanation:
I am going to treat these events as Venn probabilities, considering that:
Event A: Lying to the teacher.
Event B: Male
48% of high school students would admit to lying at least once to a teacher during the past year and that 25% of students are male and would admit to lying at least once to a teacher during the past year
This means that

Assume that 50% of the students are male.
This means that
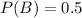
What is the probability that a randomly selected student is either male or would admit to lying to a teacher, during the past year?
This is:
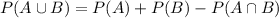
Considering the values we were given:
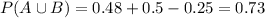
0.73 = 73% probability that a randomly selected student is either male or would admit to lying to a teacher, during the past year.