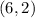Answer:
(a): The value of the objective function at the corner points
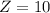
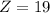
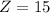
(b) The optimal solution is
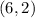
Step-by-step explanation:
Given
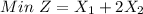
Subject to:
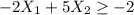 ---- 1
---- 1
 ---- 2
---- 2
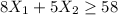 --- 3
--- 3
Solving (a): The value of the at the corner points
From the graph, the corner points are:
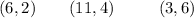
So, we have:
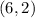 ------- Corner point 1
------- Corner point 1
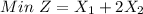
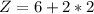
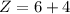
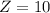
 ------ Corner point 2
------ Corner point 2
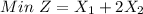
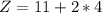
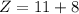
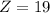
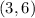 --- Corner point 3
--- Corner point 3
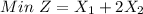
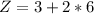
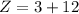
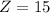
Solving (b): The optimal solution
Since we are to minimize Z, the optimal solution is at the corner point that gives the least value
In (a), the least value of Z is:
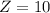
So, the optimal solution is at: corner point 1