Answer:
(a)
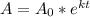
(b) There will be 1lb left after 14 hours
Explanation:
Solving (a): The equation
Since the substance decomposes at a proportional rate, then it follows the following equation

Where
 Initial Amount
Initial Amount
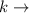 rate
rate
 time
time
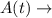 Amount at time t
Amount at time t
Solving (b):
We have:

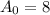

First, we calculate k using:

This gives:
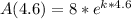
Substitute:


Divide both sides by 4
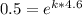
Take natural logarithm of both sides

This gives:
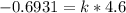
Solve for k
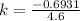
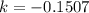
So, we have:

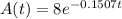
To calculate the time when 1 lb will remain, we have:
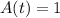
So, the equation becomes

Divide both sides by 8
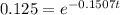
Take natural logarithm of both sides
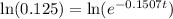
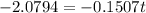
Solve for t
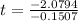
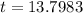
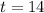 --- approximated
--- approximated