Question

A cookie factory monitored the number of broken cookies per pack yesterday.

Answer 1

Confidence Interval - 2.290 < S < 2.965

Explanation:

Complete question

A chocolate chip cookie manufacturing company recorded the number of chocolate chips in a sample of 50 cookies. The mean is 23.33 and the standard deviation is 2.6. Construct a 80% confidence interval estimate of the standard deviation of the numbers of chocolate chips in all such cookies.

Solution

Given

n=50

x=23.33

s=2.6

Alpha = 1-0.80 = 0.20

X^2(a/2,n-1) = X^2(0.10, 49) = 63.17

sqrt(63.17) = 7.948

X^2(1 - a/2,n-1) = X^2(0.90, 49) = 37.69

sqrt(37.69) = 6.139

s*sqrt(n-1) = 18.2

`s\sqrt{\frac{n-1}{X^2 _{(n-1), (\alpha )/(2) } }`
`\leq \sigma \leq s\sqrt{\frac{n-1}{X^2 _{(n-1), 1-(\alpha )/(2) } }`

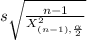
confidence interval:

(18.2/7.948) < S < (18.2/6.139)

2.290 < S < 2.965