Answer:
(a):
Dannette Alphonso

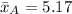
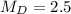

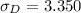

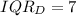
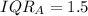
(b):
Measure of center: Median
Measure of spread: Interquartile range
(c):
There are no outliers in Dannette's dataset
There are outliers in Alphonso's dataset
Step-by-step explanation:
Given
See attachment for the appropriate data presentation
Solving (a): Mean, Median, Standard deviation and IQR of each
From the attached plots, we have:
IQR_A = 1.5 ---- Dannette
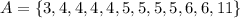 ---- Alphonso
---- Alphonso
n = 12 --- number of dataset
Mean
The mean is calculated
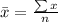
So, we have:
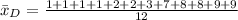

 --- Dannette
--- Dannette
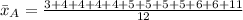
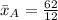
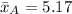 --- Alphonso
--- Alphonso
Median
The median is calculated as:
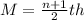
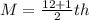
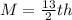
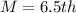
This implies that the median is the mean of the 6th and the 7th item.
So, we have:
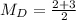
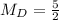
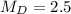 ---- Dannette
---- Dannette
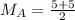
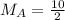
 ---- Alphonso
---- Alphonso
Standard Deviation
This is calculated as:
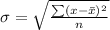
So, we have:
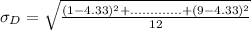
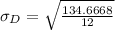
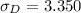 ---- Dannette
---- Dannette


 --- Alphonso
--- Alphonso
The Interquartile Range (IQR)
This is calculated as:
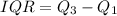
Where
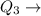 Upper Quartile and
Upper Quartile and
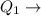 Lower Quartile
Lower Quartile
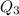 is calculated as:
is calculated as:
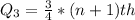

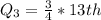
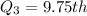
This means that
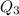 is the mean of the 9th and 7th item. So, we have:
is the mean of the 9th and 7th item. So, we have:
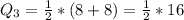
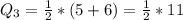
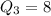 ---- Dannette
---- Dannette
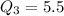 --- Alphonso
--- Alphonso
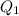 is calculated as:
is calculated as:
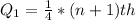


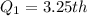
This means that
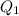 is the mean of the 3rd and 4th item. So, we have:
is the mean of the 3rd and 4th item. So, we have:
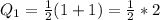
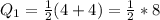
 --- Dannette
--- Dannette
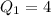 ---- Alphonso
---- Alphonso
So, the IQR is:
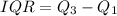
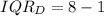
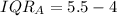
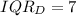 --- Dannette
--- Dannette
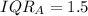 --- Alphonso
--- Alphonso
Solving (b): The measures to compare
Measure of center
By observation, we can see that there are outliers is the plot of Alphonso (because 11 is far from the other dataset) while there are no outliers in Dannette plot (as all data are close).
Since, the above is the case; we simply compare the median of both because it is not affected by outliers
Measure of spread
Compare the interquartile range of both, as it is arguably the best measure of spread, because it is also not affected by outliers.
Solving (c): Check for outlier
To check for outlier, we make use of the following formulas:
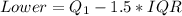
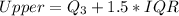
For Dannette:
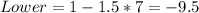

Since, the dataset are all positive, we change the lower outlier to 0.
So, the valid data range are:
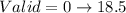
From the question, the range of Dannette's dataset is: 1 to 9. Hence, there are no outliers in Dannette's dataset
For Alphonso:
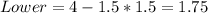
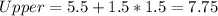
So, the valid data range are:

From the question, the range of Alphonso's dataset is: 3 to 11. Hence, there are outliers in Alphonso's dataset