Given:
The lengths of legs of a right triangle are
 and
and
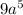 .
.
To find:
The perimeter of a right triangle.
Solution:
In a right angle triangle,
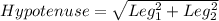
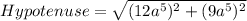
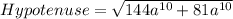

On further simplification, we get
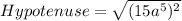
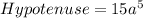
Now, the perimeter of the triangle is the sum of all of its sides.
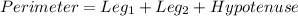
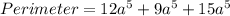
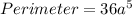
Therefore, the perimeter of the right triangle is
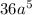 .
.