Question

Two uniform bars of the same dimensions are constructed from the same material. One bar has five evenly spaced holes through it and the second bar has only two holes. In these cases, the bars are slid over vertical pegs and rest on a horizontal surface, where friction between the bar and the surface is negligible. The two bars are each pulled by

horizontal forces of equal magnitude F from their right end as shown above. The bars' resulting angular accelerations are recorded.


Is the magnitude of the initial angular acceleration of the bar in case 1 larger than, smaller than or equal to the magnitude of the initial angular acceleration of the bar in Case 2? Explain your reasoning.

Answer 1

The angular acceleration,
`$\alpha$` is obtained from the equation of the
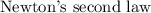`$\text{Newton's second law}$` of rotational motion,

Thus,

`$\tau = F * d$`

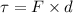
or
`$\tau = I * \alpha$`

where
`$\tau$` is torque, F is force, d is moment arm distance, I is the moment of inertia

Thus,
`$\alpha=((F* d))/(I)$`

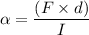
Now if the force and the moment arm distance are constant, then the
`\text{angular acceleration is inversely proportional to the moment of inertia.}`

That is when, F = d = constant, then
`$\alpha \propto (1)/(I)$` .

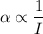Thus, moment of inertia, I is proportional to mass of the bar.

The mass is less for the bar in case (1) in comparison with that with the bar in case (2) due to the holes that is made in the bar.

Therefore, the bar in case (1), has less moment of inertia and a greater angular acceleration.