Answer: Boiling point of the given solution is
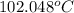 .
.
Step-by-step explanation:
Given: Molality = 2.00 m
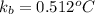
Now, equation for dissociation of water is as follows.

As it is giving 2 ions upon dissociation. So, the value of i = 2.
Formula used to calculate change in temperature is as follows.
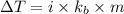
where,
i = Van't Hoff factor
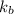 = molal boiling point elevation constant
= molal boiling point elevation constant
m = molality
Substitute the values into above formula as follows.
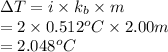
As the boiling point of water is
 . Hence, the boiling point of solution will be as follows.
. Hence, the boiling point of solution will be as follows.

Thus, we can conclude that boiling point of the given solution is
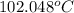 .
.