Question

What is the non-negative zero of the function f, where f(x) = 6x^2-9x-6?​

Answer 1

The non-negative zero of the function f(x) is x = 2.

Explanation:

For a given function f(x), the "zeros" of the function are the values of x such that:

f(x) = 0

In this case, we have the function:

f(x) = 6*x^2 - 9*x - 6

If we want to find the zeros of this function, we need to solve:

f(x) = 0 = 6*x^2 - 9*x - 6

To solve this, we can use the Bhaskara's formula, which says that for a general quadratic equation:

0 = a*x^2 + b*x + c

The zeros are:

`x = (-b \pm √(b^2 - 4*a*c) )/(2*a)`

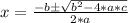
In this case our equation is:

0 = 6*x^2 - 9*x - 6

then, in the above notation, we have:

a = 6

b = -9

c = -6

Replacing these in our general formula, we get:

`x = (-(-9) \pm √((-9)^2 - 4*6*(-6)) )/(2*6) = (9 \pm 15 )/(12)`

Then we have two zeros:

x = (9 + 15)/12 = 24/12 = 2

x = (9 - 15)/12 = -6/12 = -1/2

But we want only the non-negative, so we can discard the second one.

Concluding, the non-negative zero of the function f(x) is x = 2.