Answer:
(3, 0)
Explanation:
A parabola is the locus of a point such that the distance from a fixed line called directrix and the distance from a fixed point called focus is constant.
The equation of a parabola with a vertex at (h, k) with axis of symmetry parallel to the y axis is given as:

The directrix is at y = k - p, and focus is at (h, k + p).
Given an equation -1/16(x-3)^2 + 4 = y, expressing it in standard form is:
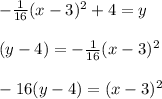
Comparing with the standard form:
The center = (h, k) = (3, 4)
Also, -16 = 4p
p = -4
Directrix is at y = k - p = 4 - (-4) = 8
Directrix is at y = 8
The focus is at (h, k + p) = (3, 4 + (-4)) = (3, 0)
The focus is at (3, 0)