Question

A small block is attached to a spring with a spring constant of 85 N/m. When the spring is compressed 0.30 meters and the released, the 0.50 kg block is launched. What is the final speed of the block?

A)
8.42 m/s

B)
3.91 m/s

C)
7.14 m/s

D)
15.3 m/s

Answer 1

Step-by-step explanation:

These Hooke's Law problems are tricky. Here's what we need to know that clears up the problem entirely. The final and also the max speed of the block will be reached at the point where the potential energy of the system is 0. So the equation we need, namely,

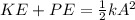`KE+PE=(1)/(2)kA^2` can be simplified down to

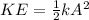`KE=(1)/(2)kA^2` and we solve this first for KE:

`KE=(1)/(2)(85)(.30)^2` and, paying NO attention whatsoever to significant digits here (because if you did the answer you get is not one of the choices)

KE = 3.825 J. Now we can use that value of kinetic energy and solve for the speed we need:

`KE=(1)/(2)mv^2` so

`3.825=(1)/(2)(.50)v^2` so

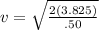`v=\sqrt{(2(3.825))/(.50) }` so

v = 3.91 m/s