Question

Determine the location and values of the absolute maximum and absolute minimum for given function : f(x)=(‐x+2)4,where 0<×<3

Answer 1

Where 0 < x < 3

The location of the local minimum, is (2, 0)

The location of the local maximum is at (0, 16)

Explanation:

The given function is f(x) = (x + 2)⁴

The range of the minimum = 0 < x < 3

At a local minimum/maximum values, we have;

`f'(x) = ((-x + 2)^4)/(dx) = -4 \cdot (-x + 2)^3 = 0`

∴ (-x + 2)³ = 0

x = 2

`f''(x) = ( -4 \cdot (-x + 2)^3)/(dx) = -12 \cdot (-x + 2)^2`

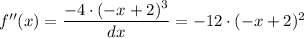
When x = 2, f''(2) = -12×(-2 + 2)² = 0 which gives a local minimum at x = 2

We have, f(2) = (-2 + 2)⁴ = 0

The location of the local minimum, is (2, 0)

Given that the minimum of the function is at x = 2, and the function is (-x + 2)⁴, the absolute local maximum will be at the maximum value of (-x + 2) for 0 < x < 3

When x = 0, -x + 2 = 0 + 2 = 2

Similarly, we have;

-x + 2 = 1, when x = 1

-x + 2 = 0, when x = 2

-x + 2 = -1, when x = 3

Therefore, the maximum value of -x + 2, is at x = 0 and the maximum value of the function where 0 < x < 3, is (0 + 2)⁴ = 16

The location of the local maximum is at (0, 16).