Question

An asphalt concrete mixture includes 94% aggregates by weight. The specific gravity of aggregate and asphalt are 2.7 and 1.0, respectively. If the bulk density of the mix is 2.317 g/cm3, what is the percent voids in the total mix?

Answer 1

The correct solution is "5.74%".

Step-by-step explanation:

The given values are:

Gravity of aggregate,

`G_(agg)=2.7`

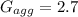
Gravity of asphalt,

`G_(asp)=1.0`

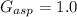
Asphalt concrete mixture,

`W_(agg)=0.94 \ W_m`

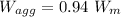
We know that,

`W_(asp)=W_m-W_(agg)`

`=0.06 \ W_m`

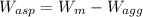
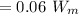
Now,

The theoretical specific gravity of mix,

⇒
`G_t=(W_(agg)+W_(asp))/((W_(agg))/(G_(agg)) +(W_(asp))/(G_(asp)) )`

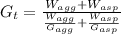
By putting the values, we get

`=(0.94 \ Wm+0.06 \ Wm)/((0.94 \ Wm)/(2.7) +(0.06 \ Wm)/(1) )`

`=2.45`

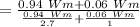
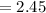
hence,

The percentage of voids will be:

⇒ %V =
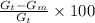
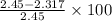
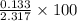
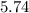`(G_t-G_m)/(G_t)* 100`

=
`(2.45-2.317)/(2.45)* 100`

=
`(0.133)/(2.317)* 100`

=
`5.74` (%)