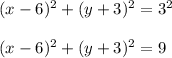Question

Determine the equation of the circle graphed below.

10
8
10
-10
-8
-6
2
-2
-4
-6
-8
-10

Answer 1

Equation = (x - 6 )² + ( y + 3 )² = 9

Explanation:

The circle passes through ( 6, 0) and ( 6 , -6)

They are the coordinates of the diameter.

Using this we can find the centre of the circle.

Find the centre of the circle.

Centre of the circle is the mid- point of (6, 0) and ( 6, -6)

`Centre = ((x_1+x_2)/(2) , (y_1 + y_2)/(2))`

`=((6 + 6)/(2), (0 + (-6))/(2))\\\\=(6, -3)`

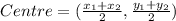
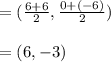
Find the radius of the circle.

`Radius = (Diameter )/(2)`

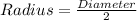
Diameter is the distance between the points (6 , 0) and ( 6, - 6)

`Diameter = √((x_2 - x_1)^2+ (y_2 - y_1)^2\\)`

`=√((6-6)^2 + (-6 -0)^2)\\\\=√(0 + 36) \\\\= 6`

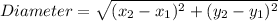
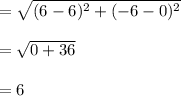
Therefore,

`Radius ,r = (6)/(2) = 3`

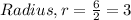
Standard equation of a circle:

`(x - a)^2 + (y - b)^2 = r^2 \ where \ (a , b) \ is \ the\ centre \ coordinates.`

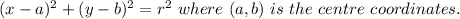
Therefore , equation of the circle ;

`(x - 6)^2 + (y + 3)^2 = 3^2\\\\(x -6)^2 + (y + 3)^2 = 9`