Question

A sample of 16 ATM transactions shows a mean transaction time of 67 seconds with a standard deviation of 12 seconds. Find the test statistic to decide whether the mean transaction time exceeds 60 seconds.

a. 1.457
b. 2.333
c. 1.848
d. 2.037

Answer 1

b. 2.333

Explanation:

Test if the mean transaction time exceeds 60 seconds.

At the null hypothesis, we test if the mean transaction time is of 60 seconds, that is:

`H_0: \mu = 60`

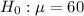
At the alternate hypothesis, we test if it exceeds, that is:

`H_1: \mu > 60`

The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

60 is tested at the null hypothesis:

This means that
`\mu = 60`

A sample of 16 ATM transactions shows a mean transaction time of 67 seconds with a standard deviation of 12 seconds.

This means that
`n = 16, X = 67, s = 12`

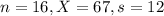
Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (67 - 60)/((12)/(√(16)))`

`t = (7)/(3)`

`t = 2.333`

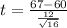
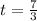
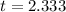
Thus, the correct answer is given by option b.